All that is comes from the mind: Pearson's correlation

Definition[edit]

Pearson's correlation coefficient is the covariance of the two variables divided by the product of their standard deviations. The form of the definition involves a "product moment", that is, the mean (the first moment about the origin) of the product of the mean-adjusted random variables; hence the modifier product-moment in the name.

For a population[edit]

Pearson's correlation coefficient when applied to a population is commonly represented by the Greek letter ρ (rho) and may be referred to as the population correlation coefficient or the population Pearson correlation coefficient. The formula for ρ^[7] is:

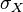\rho_{X,Y}= \frac{\operatorname{cov}(X,Y)}{\sigma_X \sigma_Y}

where:

$\operatorname{cov}$ is the covariance
$\sigma_X$ is the standard deviation of $X$

The formula for ρ can be expressed in terms of mean and expectation. Since

$\operatorname{cov}(X,Y) = \operatorname{E}[(X-\mu_X)(Y-\mu_Y)]$ ^[7]

Then the formula for ρ can also be written as

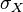\rho_{X,Y}=\frac{\operatorname{E}[(X-\mu_X)(Y-\mu_Y)]}{\sigma_X\sigma_Y}

where:

$\operatorname{cov}$ and $\sigma_X$ are defined as above
$\mu_X$ is the mean of $X$
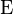$\operatorname{E}$ is the expectation.

The formula for ρ can be expressed in terms of uncentered moments. Since

$\mu_X=\operatorname{E}[X]$
$\mu_Y=\operatorname{E}[Y]$
$\sigma_X^2=\operatorname{E}[(X-\operatorname{E}[X])^2]=\operatorname{E}[X^2]-\operatorname{E}[X]^2$
$\sigma_Y^2=\operatorname{E}[(Y-\operatorname{E}[Y])^2]=\operatorname{E}[Y^2]-\operatorname{E}[Y]^2$
$\operatorname{E}[(X-\mu_X)(Y-\mu_Y)]=\operatorname{E}[(X-\operatorname{E}[X])(Y-\operatorname{E}[Y])]=\operatorname{E}[XY]-\operatorname{E}[X]\operatorname{E}[Y],\,$

Then the formula for ρ can also be written as

\rho_{X,Y}=\frac{\operatorname{E}[XY]-\operatorname{E}[X]\operatorname{E}[Y]}{\sqrt{\operatorname{E}[X^2]-\operatorname{E}[X]^2}~\sqrt{\operatorname{E}[Y^2]- \operatorname{E}[Y]^2}}.

For a sample[edit]

Pearson's correlation coefficient when applied to a sample is commonly represented by the letter r and may be referred to as the sample correlation coefficient or the sample Pearson correlation coefficient. We can obtain a formula for r by substituting estimates of the covariances and variances based on a sample into the formula above. So if we have one dataset {x₁,...,x_n} containing n values and another dataset {y₁,...,y_n} containing n values then that formula for r is:

r = r_{xy} =\frac{\sum ^n _{i=1}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum ^n _{i=1}(x_i - \bar{x})^2} \sqrt{\sum ^n _{i=1}(y_i - \bar{y})^2}}

where:

$n, x_i, y_i$ are defined as above
$\bar{x}=\frac{1}{n}\sum_{i=1}^n x_i$ (the sample mean); and analogously for $\bar{y}$

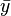
Rearranging gives us this formula for r:

r = r_{xy} =\frac{n\sum x_iy_i-\sum x_i\sum y_i} {\sqrt{n\sum x_i^2-(\sum x_i)^2}~\sqrt{n\sum y_i^2-(\sum y_i)^2}}.

where:

$n, x_i, y_i$ are defined as above
This formula suggests a convenient single-pass algorithm for calculating sample correlations, but, depending on the numbers involved, it can sometimes be numerically unstable.

Rearranging again gives us this^[7] formula for r:

r = r_{xy} =\frac{\sum x_iy_i-n\bar{x}\bar{y}} {\sqrt{(\sum x_i^2-n\bar{x}^2)}~\sqrt{(\sum y_i^2-n\bar{y}^2)}}.

where:

$n, x_i, y_i, \bar{x}, \bar{y}$ are defined as above

An equivalent expression gives the formula for r as the mean of the products of the standard scores as follows:

r = r_{xy} =\frac{1}{n-1} \sum ^n _{i=1} \left( \frac{x_i - \bar{x}}{s_x} \right) \left( \frac{y_i - \bar{y}}{s_y} \right)

where

$n, x_i, y_i, \bar{x}, \bar{y}$ are defined as above, and $s_x, s_y$ are defined below
$\left( \frac{x_i - \bar{x}}{s_x} \right)$ is the standard score (and analogously for the standard score of y)

Alternative formulae for r are also available. One can use the following formula for r:

r = r_{xy} =\frac{\sum x_iy_i-n \bar{x} \bar{y}}{(n-1) s_x s_y}

where:

$n, x_i, y_i, \bar{x}, \bar{y}$ are defined as above and:
$s_x=\sqrt{\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})^2}$ (the sample standard deviation); and analogously for s_y

Algorithms.of.the.Intelligent.Web

private static final double ZERO = 0.0d;



    int n;



    double[] x;

    double[] y;



    public PearsonCorrelation(Dataset ds, Item iA, Item iB) {



        double aAvgR = iA.getAverageRating();

        double bAvgR = iB.getAverageRating();



        Integer[] uid = Item.getSharedUserIds(iA, iB);

        n = uid.length;

        x = new double[n];

        y = new double[n];



        User u;

        double urA=0;

        double urB=0;



        for (int i=0; i<n; i++) {



            u = ds.getUser(uid[i]);

            urA = u.getItemRating(iA.getId()).getRating();

            urB = u.getItemRating(iB.getId()).getRating();



            x[i] = urA - aAvgR;

            y[i] = urB - bAvgR;

        }

    }



    public PearsonCorrelation(double[] x, double[] y) throws java.lang.IllegalArgumentException {



        if (x.length != y.length) {

            throw new IllegalArgumentException("Arrays x and y should have the same length!");

        }



        n = x.length;

        //System.out.print("N="+n);



        this.x = x;

        this.y = y;

    }



    public double calculate() {



        if( n == 0) {

            return 0.0;

        }



        double rho=0.0d;



        double avgX = getAverage(x);

        double avgY = getAverage(y);



        double sX = getStdDev(avgX,x);

        double sY = getStdDev(avgY,y);



        double xy=0;



        for (int i=0; i < n; i++) {



            xy += (x[i]-avgX)*(y[i]-avgY);

        }

        //No variation -- all points have the same values for either X or Y or both

        if( sX == ZERO || sY == ZERO) {



            double indX = ZERO;

            double indY = ZERO;



            for (int i=1; i < n; i++) {



                indX += (x[0]-x[i]);

                indY += (y[0]-y[i]);

            }



            if (indX == ZERO && indY == ZERO) {

                // All points refer to the same value

                // This is a degenerate case of correlation

                return 1.0;

            } else {

                //Either the values of the X vary or the values of Y

                if (sX == ZERO) {

                    sX = sY;

                } else {

                    sY = sX;

                }

            }

        }



        rho = xy / (n*(sX*sY));



        return rho;

    }

    private double getAverage(double[] v) {

        double avg=0;



        for (double xi : v ) {

            avg += xi;

        }



        avg = avg/v.length;



        //System.out.print("Average: "+avg);

        return avg;

    }



    private double getStdDev(double m, double[] v) {

        double sigma=0;



        for (double xi : v ) {

            sigma += (xi - m)*(xi - m);

        }



        sigma = sigma / v.length;



        //System.out.print("StdDev: "+Math.sqrt(sigma));

        return Math.sqrt(sigma);

    }

Colored by Color Scripter
cs

Programming Collective Intelligence

public double sim_pearson (Map < String, Map < String, Double >> personalRate, String person1, String person2) {

        Map<String, Double> Si = new HashMap<String, Double>();

        double result = 0;

        double sumP1 = 0;

        double sumP2 = 0;

        double sumP1Sq = 0 ;

        double sumP2Sq = 0 ;

        double pSum = 0;

        double pScore = 0 ;

        double num = 0;

        double den = 0 ;

        for (Map.Entry<String, Double> item : personalRate.get(person1).entrySet()) {

            for (Map.Entry<String, Double> item2 : personalRate.get(person2).entrySet()) {

                if (item.getKey().equals(item2.getKey())) {

                    Si.put(item.getKey(), 1.0);

                }

            }

        }

        for ( Map.Entry<String,Double> matchedItem : Si.entrySet()) {

            sumP1 += personalRate.get(person1).get(matchedItem.getKey());

            sumP2 += personalRate.get(person2).get(matchedItem.getKey());

            sumP1Sq += Math.pow(personalRate.get(person1).get(matchedItem.getKey()), 2);

            sumP2Sq += Math.pow(personalRate.get(person2).get(matchedItem.getKey()), 2);

            pSum += (personalRate.get(person1).get(matchedItem.getKey())*personalRate.get(person2).get(matchedItem.getKey()));

        }

        num = pSum-(sumP1*sumP2/Si.size());

        den = Math.sqrt((sumP1Sq - Math.pow(sumP1 ,2)/Si.size())*(sumP2Sq - Math.pow(sumP2, 2)/Si.size()));

        if (den==0) result = 0;

        else result = num/den;

        return result;

    }

Colored by Color Scripter
cs

All that is comes from the mind

전체 페이지뷰

2015년 12월 9일 수요일

Pearson's correlation

Definition[edit]

For a population[edit]

For a sample[edit]

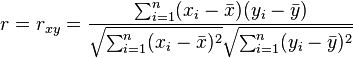
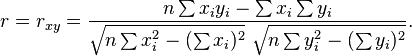
댓글 없음:

댓글 쓰기